初一概率题应选择圆规或者套尺进行测量后,求出其值,并且找到其中位数,或者平均值进行计算。
1.十几乘十几:口诀:头乘头,尾加尾,尾乘尾。
例:12×14=?
解:1×1=12+4=62×4=812×14=168
注:个位相乘,不够两位数要用0占位。
2.头相同,尾互补(尾相加等于10): 口诀:一个头加1后,头乘头,尾乘尾。
例:23×27=?
解:2+1=32×3=63×7=2123×27=621
注:个位相乘,不够两位数要用0占位。
3.第一个乘数互补,另一个乘数数字相同:口诀:一个头加1后,头乘头,尾乘尾。
例:37×44=?
解:3+1=44×4=167×4=2837×44=1628
注:个位相乘,不够两位数要用0占位。
4.几十一乘几十一:口诀:头乘头,头加头,尾乘尾。
例:21×41=?
解:2×4=82+4=61×1=121×41=861
5.11乘任意数:口诀:首尾不动下落,中间之和下拉。
例:11×23125=?
解:2+3=53+1=41+2=32+5=7 2和5分别在首尾 11×23125=254375
注:和满十要进一。觉得有用点个赞吧
概率实质上就是两个计数原理的问题完成一件事有不同种办法,每种办法又有不同的方法;这样完成这件事所有的方法数就要把每种办法中的方法都加起来(加法原理)。如果完成一件事分不同的步骤,每一步又有不同的方法;这样完成这件事所有的方法数就要把所有步骤中的方法都乘起来(乘法原理)
1、核心题型之古典概型题眼:无概率求概率(一次性试验)解题步骤:
(1)求解总的情况数(利用组合数或是排列数);(2)求解目标情况数(常用的求解方法为穷举法(数字)、组合数或是排列数)
一求甲三次投篮恰好得三分的概率三次只有一次投中 C3(1)1/3(1-1/3)(1-1/3)=4/9
二假设甲投一次,乙投两次,设X是甲这次投篮的得分减去乙这两次投篮得分总和的差,求随机变量x的分布列. 甲有0分或3分 (0分,2/3,3分,1/3)乙有可能得0分或3分,或6分(0分,9/16,3分,6/16,6分,1/16 所以x取值是0,-3分,-6分,3分。0分,甲0分,乙0分,甲3分,乙3分,2/3*9/16+1/3*6/16=1/2 -3分,甲0分,乙3分,甲3分,乙6分,2/3*6/16+1/3*1/16=13/48 -6分,甲0分,乙6分, 2/3*1/16=1/24 3分,甲3分,乙0分 1/3*9/16=3/16
---------------------------------------------------------------------------------
方法一:列举法
1. 列表:适用于一步概率计算
例1 一个不透明的袋子中装有黑、白小球各两个,这些小球除颜色外无其他差别,从袋子中随机摸出一个小球后,放回并摇匀,再随机摸出一个小球,则两次摸出的小球都是白球的概率为____.

2. 画树状(形)图:适用于两步及以上概率计算
例2 在排球训练中,甲、乙、丙三人相互传球,由甲开始发球(记作为第一次传球),则经过三次传球后,球仍回到甲手中的概率是()

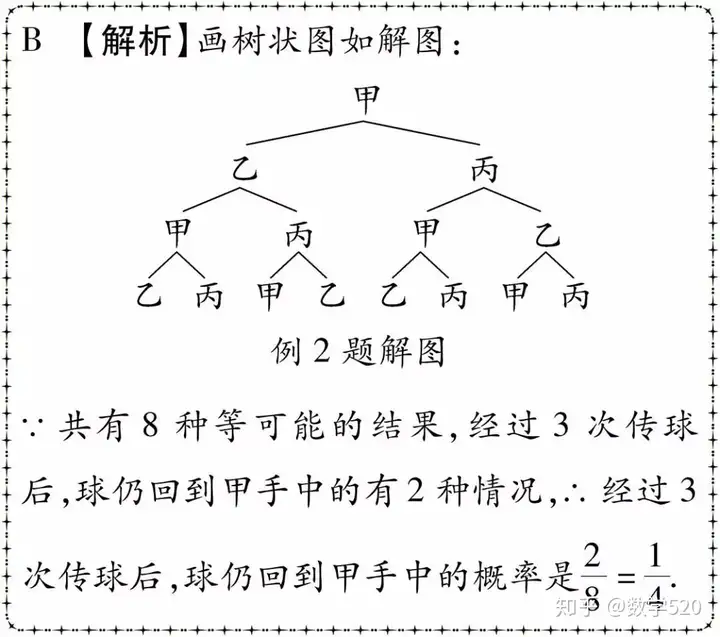
方法二:频率估计概率
例3 林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组统计数据:
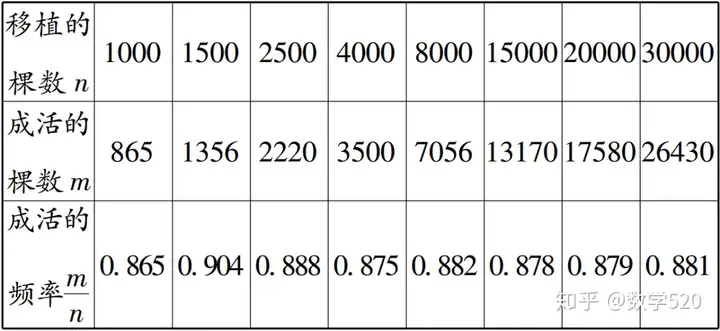
估计该种幼树在此条件下移植成活的概率为____.

方法三:几何面积概型
例4 如图所示的圆面图案是用相同半径的圆与圆弧构成的,若向圆面投掷飞镖,则飞镖落在黑色区域的概率为____.
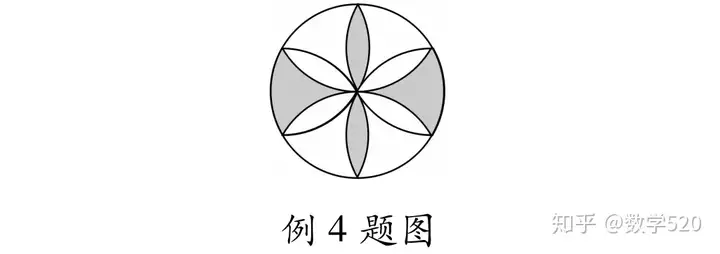

应用:游戏公平性问题
例5 一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同.甲、乙两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有等可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
